How to calculate the cutting length of triangular stirrups? / Cutting length of samosa ring.

 If you are looking for a readymade calculator for triangular stirrups, then click here.

 For the calculation procedure, go through the following steps.👇

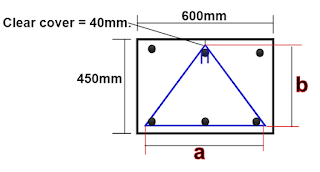
Let us now calculate the cutting length of triangular stirrups as shown below.

Given data:

Column width = 600mm.

Column depth = 450mm.

Clear cover = 40mm.

Stirrup dia. = d = 8mm.

The cutting length of the triangular stirrup is calculated by the formula

=[ (2 × H ) + a + (2nos.× hook length) - ( 4nos. × above 90° bend.)]

First, we will calculate the value of a & b as shown in the above drawing.

Here,

 a =[( column width ) - (2nos × clear cover) - (2nos. × 1/2 dia. of the stirrup)].

For a clear understanding, I have redrawn the triangular stirrup separately as shown below.

a = [ (600mm ) - ( 2nos. × 40mm ) - ( 2nos. × 1/2 × 8mm )]

   = [ 600mm - 80mm - 8mm ]

   = 512mm.

b = [( column depth ) - (2nos × clear cover) - (2nos. × 1/2 dia. of the stirrup)].

    = [ ( 450mm ) - ( 2nos. × 40mm ) - ( 2nos. × 1/2 × 8mm )]

    = [ 450mm - 80mm - 8mm]

    = 362mm.

The cutting length of the triangular stirrup

= [ (2 × H ) + a + (2nos.× hook length) - ( 4nos. × above 90° bend.)]

H =√( a/2 )2 +( b )2

[ H is a hypotenuse of a (half ) triangle ]

=√( 512/2 )2 +( 362 )2

=√65536 +131044

= √ 196580

=443.373 mm.

The triangular stirrup cutting length

= [ ( 2 × 443.373 ) + 512mm + ( 2nos. × 10d ) - ( 4nos.× 3d )]

{Here, 10d is taken as hook length , 3d for the bend above 90°, & d is stirrup bar dia.}

= [ 886.746 + 512mm + ( 2nos.× 10 × 8mm ) - ( 4nos.× 3× 8mm )

= [1398.746 mm + 160mm - 96mm.]

= 1462.746mm = 1.462m.

Note: Bend above 90° 👉 (2nos. of the hook bend + 2nos.) on the other two stirrup corners.

  For BBS & cutting length of all types of structural members, click here.  

 If you have any quarries, you can ask me in the comment box👇.

Thank you for going through this article❤. Have a good day😄.

Share: